🎶 這是好和弦的「音律的故事」系列的第 6 篇文章,總共有 6 篇。
前情提要
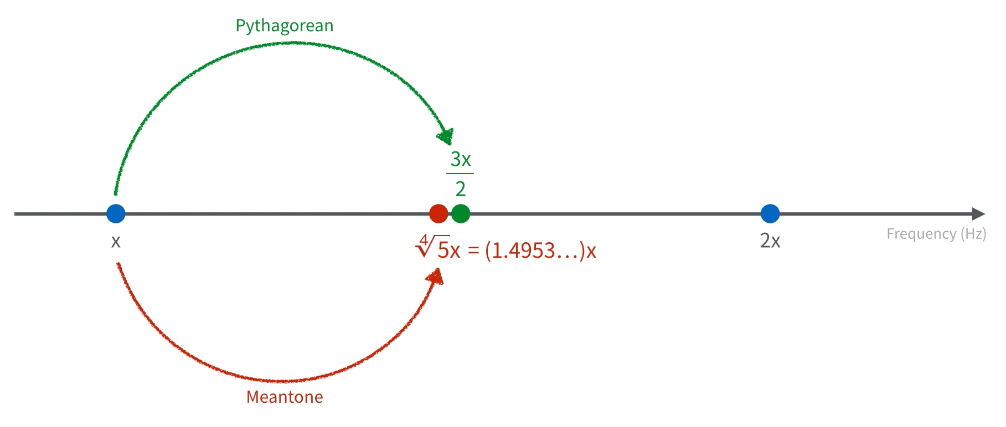
在上一篇文章,我提到了畢達哥拉斯音律中的完全五度,例如 Do-Sol 這樣的組合會很和諧。但大三度音程,像是 Do-Mi 的組合就沒那麼好聽,因為在畢達哥拉斯音律中,Do-Mi 的頻率不是簡單的整數比。
到了大約 16 世紀,隨著音樂逐漸需要使用 Do-Mi 這樣的三度音程,人們發明了一種偏好三度音程的音律系統,稱為「中庸全音律」(meantone temperament)。
中庸全音律可以讓 Do-Mi 的組合變得更好聽,因為它把 Do-Mi 的頻率比例「強制設定」成 4:5。但這樣的調整的副作用就是犧牲了 Do-Sol 的協和程度,因為在中庸全音律中,Do-Sol 的頻率比例變成了 1:∜5,也就是大約 1:1.4953。
而且,中庸全音律同樣沒有解決已經存在超過一千年的「狼音」問題,使得作曲家在寫曲時,還是需要左閃右躲地避開某些會很難聽的音程組合。
如果你是從前幾篇文章一路讀過來的,你應該想問這個問題很久了:
「阿到底是還要多久阿?就沒有辦法一次讓全部的音程組合都很好聽嗎?」
答案可能會出乎你的意料:「還真的是沒有辦法。」
因為如果要讓某兩個音的頻率組合形成簡單整數比,勢必就會動到另一個組合。不管你如何調整,永遠都沒有辦法讓全部的組合都形成完美的簡單整數比。
其實不平均的「平均律」
在中庸全音律以及之前的音律系統中,都是優先照顧某一種特定的音程組合,讓那個組合很協和,然後放任其他的組合讓它們很難聽。
因此,18 世紀的音樂學家們決定要改變思維:既然沒有辦法讓全部的音程組合都聽起來很協和,那麼我們就改成讓所有的組合都只有一點點不協和吧!這樣的話,搞不好聽眾根本就不會注意到?
於是,所謂的「平均律」(well temperament)就誕生了。這裡的「平均律」指的不是一種特定的音律,而是泛指各種「不論彈哪種音程、和弦、調性,都不會非常難聽」的音律系統們。
這些「平均律」系統,基本上都是用「人為主觀判斷」的方式產生的。各個音樂學家用他們覺得好聽的方法,把某個音調高一點點、某個音降低一點點⋯⋯互相橋來橋去,直到所有的音程組合聽起來「好像」都不會太難聽為止。
幾個著名的平均律系統包括:
- Kirnberger temperament,由巴赫的學生 Johann Kirnberger 所制定。
- Werckmeister temperament,由管風琴家 Andreas Werckmeister 所制定。
- Young temperament,由科學家 Thomas Young 所制定。

我沒有打算在這邊詳細介紹它們的些微差異,總之這三種有名的調律方法,都可以算是我們現在中文說的「平均律」。但正如我剛才所說的,這些被通稱為「平均律」的調律方式,都是根據制定者自己的品味設定的。它們的每一個半音的音程寬度,並不是完全平均的。
那到底一開始是誰把它翻譯成「平均律」的阿?其實我也不知道,但是他很顯然地用錯字了。
算盤神
到這邊為止,你可能會想,這些音樂學家是很笨嗎?為什麼還要繁瑣地調整每個音高?為什麼不讓全部的音高都平均分配就好了呢?其實他們不是故意的,他們無法這樣做的原因,是因為他們不會開根號。
要把一個八度分成平均分佈的 12 個音,就必須找到一個特定的比例,使得這個比例的 12 次方剛好等於 2。換句話說,就是需要找到「2 的 12 次方根」。
當然現在你只要打開計算機 app 一按就可以得到答案了,不過對於 17 世紀的人來說,算出 2 的 12 次方根簡直是比登天還難阿!不過有個厲害的人,他還真的登天了。
在中國明朝,有個名叫朱載(ㄗㄞˇ)堉的宅男,他除了是天文學家、物理學家、數學家、音樂家、舞學家、作家、樂器製造師之外,他還是個「算盤神」。
他竟然利用一個有 81 位數的算盤,計算出了 2 的 12 次方根,精確到小數點後 24 位,找到了真正的「平均律常數」:1.059 463 094 359 295 264 561 825。

題外話,朱載堉不只是地球上第一個算出平均律常數的人,他也很可能也是地球上第一個做出舞蹈教學 GIF 動畫的人⋯⋯才怪。
真正的平均律是「等律」(equal temperament)
總之,有了平均律常數之後,我們只要隨便找一個音,當作是哪一個音名都可以,把它的頻率乘上平均律常數,就可以得到高半音的頻率。重複這個步驟 12 次,第 13 的音的頻率就會剛剛好是第 1 個音的兩倍,因為平均律常數的定義就是 2 的 12 次方根。這就是我們現代使用的、把八度完全均等分成 12 等份的音律系統。

但因為「平均律」這個詞已經被用掉了,所以我們現在把這個「真正平均的」音律系統稱為「等律」(equal temperament)。雖然早在明朝的時候,朱載堉就已經算出等律的理論,但等到它能夠在鍵盤樂器上實作出來,已經是快要 20 世紀的時候的事了。
全部一起比較
最後我要用整個系列提到過的各種音律系統,彈一小段音樂片段給你聽。我會盡量使用很多複雜和弦,這樣也許比較能曝露早期調律法的缺點,看看你能不能聽出各種系統的細微差別。
首先是畢達哥拉斯的音律:
然後是 16 世紀之後開始流行的中庸全音律:
接下來是三種不同的所謂的平均律系統,首先是巴赫的學生 Kirnberger 的版本:
再來是管風琴家 Werckmeister 的版本:
然後是科學家 Thomas Young 的版本:
最後是我們現代使用的,用 2 的 12 次方根來調音的「等律」:
喜歡這篇文章嗎?
這篇文章也有影片版 → WiwiVideo | YouTube
如果覺得我的文章和影片對你有幫助,希望你可以藉由購買我的《鋼琴技巧急診室》和《即興幼幼班》課程、實體書、大包裝、加入頻道會員,或至少在社群媒體分享這篇文章,以實際行動來幫助好和弦的持續運作。謝謝你!
也希望你可以使用 E-mail 訂閱我,這樣才不會錯過我的最新內容喔!